*** 모바일 앱 환경에서는 라텍스 공식이 깨져서 나오니 가급적 웹 환경에서 읽어주시길 바랍니다. 🙂 ***
“선형대수, 확률과 통계, 분석복습”
이 게시물에서는 선형 대수학에 대한 두 번째 기사를 게시할 것입니다.
딥 러닝을 위한 선형 대수학을 검토하는 첫 번째 기사는 아래 링크에서 찾을 수 있습니다.
https://kyteris0624.14
딥 러닝 자세히 알아보기 3부. 기본 딥 러닝 수학
*** 모바일 앱 환경에서는 라텍스 공식이 깨져보이니 가급적 웹 환경에서 읽어주세요 🙂 *** “선형대수학, 확률과 통계학, 미적분학 복습”
kyteris0624.tistory.com
이 기사에서
1. 만약 $Ax = b$가 유일한 해결책으로 결정된다면, 즉 $x = A^{-1}b$가 결정된다면(= $A$의 역행렬이 존재한다면)?
계속하고 싶다
우선, $A^{-1}$는 언제 존재합니까?
$A \in \mathbb{R}^{n \times n}$ 중에서 정답을 먼저 말합니까? 모든 열 벡터(행 벡터)는 선형적으로 독립적입니다.이면 역행렬이 있습니다.
그렇다면 선형 독립은 무엇입니까?
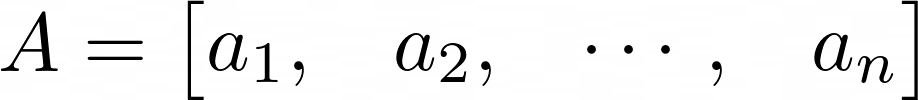
* 선형 독립
위 그림에서 $A$는 열 벡터의 배열로 표현됩니다. 각 열 벡터는 $a_i \in \mathbb{R}^n$입니다.

행렬($A$)과 벡터($x$)의 곱셈을 행렬의 열 벡터의 선형결합이라 하고 위 식은 $Ax= 0$이다.
이제 $A$의 열 벡터가 선형 독립이면 위 방정식을 만족하는 해가 영 벡터일 뿐이라면, 즉 모든 $x_i$가 0일 때만 위 방정식을 만족한다면 다음과 같은 열을 갖게 됩니다. $A$ 우리는 벡터가 선형적으로 독립적이라고 말합니다.
그리고 이 경우에만 $A$의 역행렬이 존재합니다.
선형 종속는 선형 독립의 반대입니다. $A$의 열 벡터는 0이 아닌 솔루션이 있는 경우 선형 종속입니다.
즉, $x_i$가 0이 아닌 해가 하나 이상 있으면 선형 종속입니다.
이제 $A$의 열 벡터가 모두 선형 독립이면 역행렬이 존재하는 이유는 무엇입니까?
이를 위해 벡터 공간, 기저, 차원의 개념을 알아야 합니다.
* 벡터 공간, 기저, 차원
위의 선형 조합을 참조하십시오. 결과 선형 조합 연산은 벡터입니다. ($Ax = 0$)에서 $0$도 숫자가 아니라 0 벡터입니다.
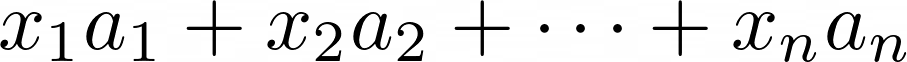
위의 연산에서 $a_1, \cdots 및 a_n$ 벡터가 ‘선형 독립’이라고 가정하고 다음으로 넘어갑시다.
그러면 $a_1, \cdots, a_n$이 나에게 주어진 n개의 벡터이고 $x_1, \cdots, x_n$가 랜덤 스칼라라면,
위의 작업에서 발생할 수 있는 벡터는 무한합니다.
그리고 그 결과로 가능한 모든 벡터의 집합을 ‘벡터 공간’이라고 합니다.
요약하면, 벡터 공간은 $n $ 선형 독립 벡터의 선형 조합으로 생성될 수 있는 벡터의 집합이며,
반대로 벡터 공간의 재료 역할을 하는 $n$ 벡터를 ‘기저’ 벡터라고 합니다.
차원은 기저 벡터의 수입니다.
즉, 위의 예에서 벡터 공간의 차원은 $n$ 차원입니다.
하지만 위의 방정식을 $Ax$로 본다면? 마지막으로 $A$는 열 벡터의 선형 조합 집합입니다. 이를 위해 행렬 A’가 있습니다.열 공간그리고 그것이 지금 이야기의 핵심입니다.
원래 이야기로 돌아가서 $A$의 모든 열 벡터가 선형 독립이면 역행렬이 존재합니다.
즉, $Ax = b$의 솔루션은 고유합니다. 그러나 $x\in \mathbb{R}^n$은 $b\in \mathbb{R}^n$와 같기 때문입니다.
그러나 $A$의 열 공간 차원은 $n$ 차원이므로 벡터 $b$는 벡터 공간의 요소가 될 수밖에 없다.
1. $Ax = b$의 해는 유일하다. (해는 $x = A^{-1}b$입니다.)
2. $A$의 역행렬이 존재합니다.
3. $A$의 열 벡터(또는 행 벡터)는 모두 선형 독립입니다.
4. $A$의 컬럼 스페이스의 차원은 n이다 = 즉 벡터 $b$는 컬럼 스페이스의 요소이다.
5. $A$의 순위는 n이다.
모두 정확히 동등한 문장입니다. 하나가 참이면 나머지 네 개는 참이다.
여기서 순위는 선형 독립 열 벡터(또는 행 벡터)의 수입니다.
지금까지 The Sun Is One과 관련된 기본적이고 중요한 개념을 요약했습니다.
그렇다면 “누락된 솔루션의 경우”에 대한 대략적인 솔루션을 어떻게 얻을 수 있습니까?
“해가 없을 때”는 다음과 같습니다.
1. $Ax = b$에 대한 솔루션은 없습니다.
2. $A$의 역행렬이 존재하지 않습니다.
3. $A$의 열 벡터는 선형 종속입니다.
4. $A$의 열 공간의 차원이 n보다 작음 = 즉, 벡터 $b$는 열 공간의 요소가 아닙니다. (열 공간에 포함되지 않음)
5. $A$의 순위는 n보다 작습니다.
그래서 우리는 무엇을 원합니까 ‘예쁜’ (근사해), 최적의 근사해를 결정하기 위한 기준이 있어야 하며,
결국 무엇 작은 실수’수단
즉, $x$는 $\lVert Ax-b \rVert^2$를 최소화하기 위한 최상의 솔루션입니다.
이는 궁극적으로 $b$ 벡터와 $A$ 행렬의 열 공간 사이의 ‘거리’가 최소화되어야 함을 의미합니다.

위 그림에서 $Col(A)$는 A의 열 간격을 의미합니다.
벡터 $b$는 A의 열 공간 밖에 있고 $A \hat{x}$와 $b$ 사이의 최소 거리는 수직 거리이므로 ‘vertical’이 포함됩니다.
이것은 두 벡터 $A \hat{x}$와 $A \hat{x} – b$가 서로 직교한다는 것을 의미합니다.
$x$가 아닌 $\hat{x}$로 표현한 이유는 정확한 해가 아닌 근사해를 구하기 위함이라 변경하였다.
직교인 경우 ‘내적 = 0’그리고 이를 식으로 표현하고 계산을 진행하면 다음과 같은 결과가 나옵니다.
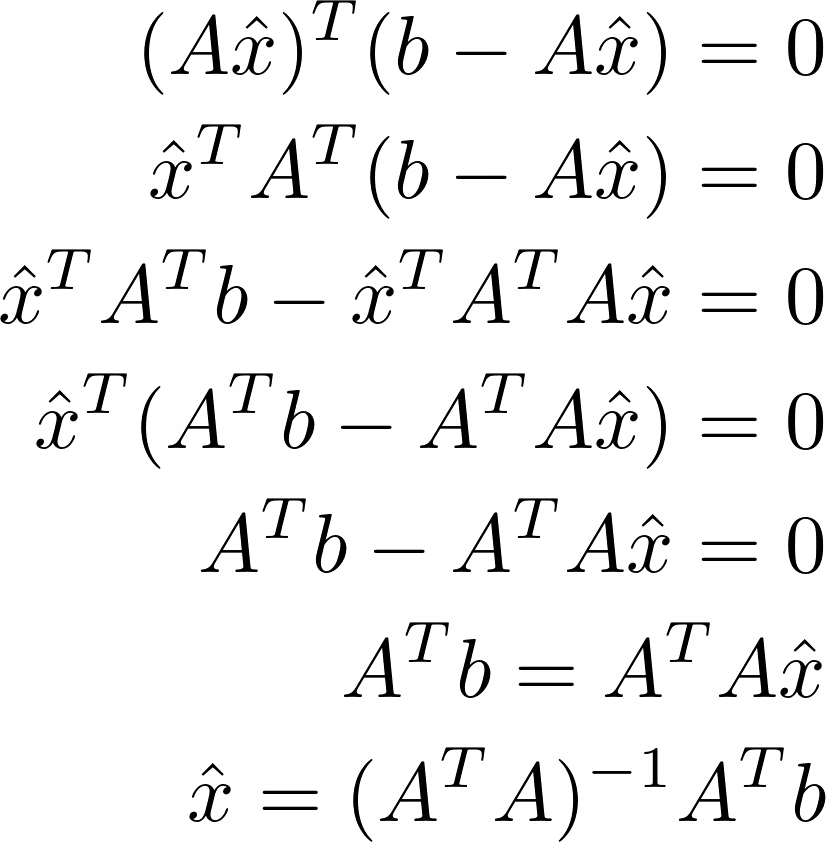
물론 여기에도 요구 사항이 있습니다. $(A^TA)$의 역행렬이 존재합니다.
존재하는 경우 위와 같이 $\hat{x}$를 얻을 수 있습니다.
$\hat{x}$가 null이 아닌 벡터라는 것이 의미가 있기 때문에 $\hat{x}$가 null 벡터가 아니라는 가정하에 4행에서 5행은 건너뜁니다.
여기 선형 대수학에서 중요한 행렬$A^TA$가 나타납니다.
1. $A$의 형태가 무엇이든(즉, 정방행렬이든 아니든) 항상 정방행렬입니다.
2. 항상 대칭 행렬입니다. 즉, $(A^TA)^T = A^TA$입니다.
3. $A$의 열 벡터가 서로 선형적으로 독립적인 경우(2차이든 아니든) $A^TA$는 항상 양의 정부호 행렬입니다.
4. $(A^TA)^{-1}$가 존재하면 $A$의 열 벡터는 선형 독립입니다. (정사각 행렬이든 아니든)
5. $A^TA$의 고유값은 0보다 큽니다.
6. $A$가 직교 행렬이면 $A^T$는 $A$의 역행렬이므로 $A^TA = I$입니다.
여기에 우리의 두 번째 목적 방정식인 양의 정부호 행렬인 고유값이 나타났습니다.
$Ax = \lambda x$를 참조합니다.
다음 포스트로 옮기도록 하겠습니다. (너무 길다고 생각했는데…)